Two lines are perpendicular if they meet at 90º (right-angle).
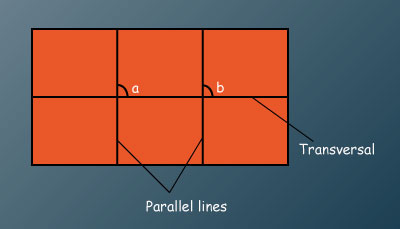
Lines that do not meet at all are said to be parallel.

We can make a transversal by drawing a line cutting the parallel lines.
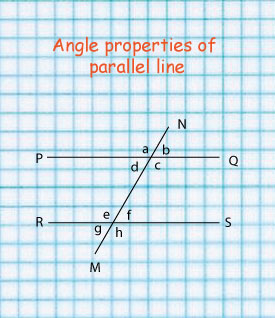
If PQ and RS in the figure above are parallel and MN is a transversal then:
In the figure shown below AB, CD and EF are parallel. Find angles x, y, z and q
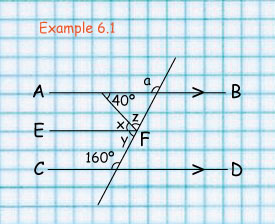
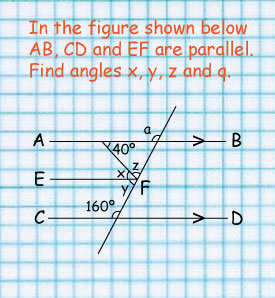

The sum of angles on a straight line is 180 degrees.

In the figure shown, AB and CD are parallel. Find angles p and q.

Perpendicular and parallel lines can be drawn using a ruler and a pair of compasses.


Some important constructions are discussed below.
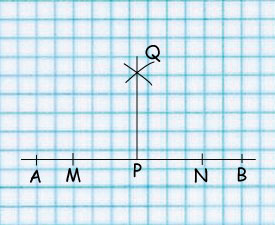
1. Draw arcs with centre P and a radius to cut AB at M and N.
2. Draw arcs with centres M and N and a radius greater than PM such that the arcs meet at Q.
3. Draw QP the required perpendicular.
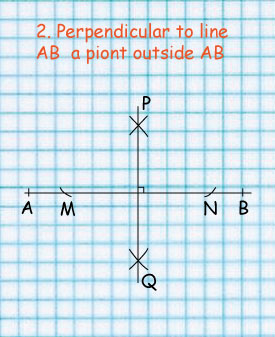
1. Draw arcs with centre P and a radius to cut AB at M and N.
2. Draw arcs with centres M and N and a radius such that the arcs meet at Q and P.
3. Draw PQ the required perpendicular.
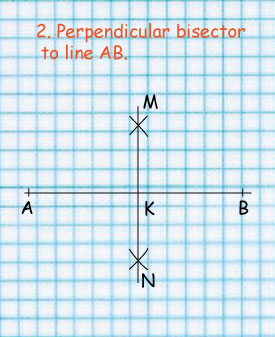
1. Draw arcs with centres A and B and a radius greater than 1/2 AB such that the arcs meet at M and N.
2. Draw MN to meet AB at K. MN is the perpendicular bisector and K is the mid point of AB.
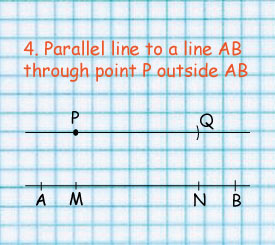
1. Mark two points M and N on AB.
2. Draw an arc with centre P and radius MN.
3. Draw an arc with centre N and radius MP to cut the first arc at Q.
4. Draw PQ the required parallel line.
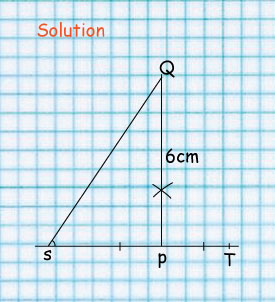
P is a point on line ST. P is 4 cm from S.
Draw a perpendicular to ST from P. Mark a point Q on the perpendicular such that Q is 6 cm above P join SQ. Measure SQ and ∠QSP.
1. On triangle PQR below, draw bisector of angle PQR. Draw a perpendicular from P to this bisector. The perpendicular meets the bisector at S. What is the length of PS?

A. 4.0 cm B. 4.5 cm C. 7.8 cm D. 7.2 cm
2. N is a point on line AB. Draw a perpendicular to AB passing through N. Mark point C on the perpendicular 9.2 cm above N. Join AC and BC.
What is the size of the angle ACN?
A. 1530 B. 600 C. 270 D. 330
3. The line AB given below is one of the sides of triangle ABC in which AC = 6 cm and angle CAB = 1200. Complete the construction of the triangle. Draw the bisector of angle ABC and the perpendicular bisector of the line BC. The two bisectors of the line BC. The two bisectors meet at X.

What is the size of angle AXB?
A. 580 B. 830 C. 970 D. 1070
4. X is a point on line AB. Construct XY perpendicular to AB through X. Draw XAY = 550 such that line AY meets the perpendicular at Y. Bisect angle XAY. Let the bisector meet YX at Z.
What is the length of YZ?
A. 3.6 cm B. 7.9 cm C. 7.0 cm D. 6.4 cm
5. On triangle XYZ below, draw a bisector of angle XYZ. Draw a perpendicular from X to this bisector. Let the perpendicular meet the bisector at N.
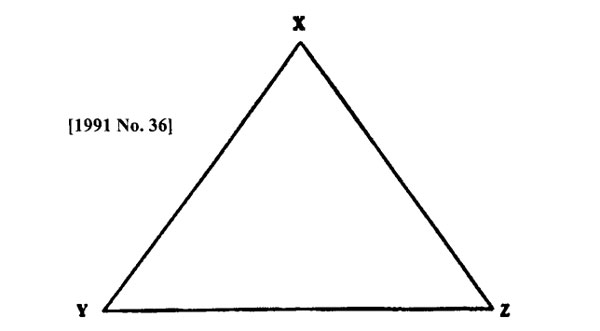
What is the length of XN?
A. 3.7 cm B. 4.2 cm C. 5.5 cm D. 7.3 cm
6. On triangle XYZ below, construct a perpendicular from X to meet line YZ at M. Construct a perpendicular bisector of line XY and let this bisector meet line MX at N.
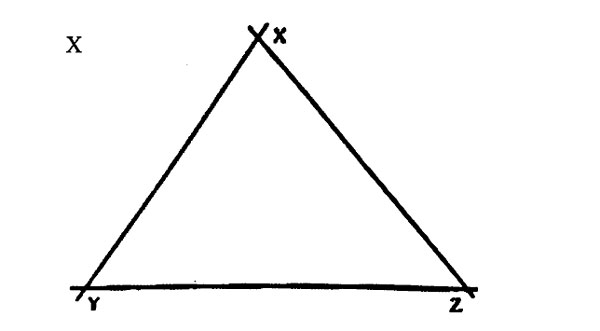
What is the length of XN?
A. 3.3 cm B. 1.2 cm C. 4.5 cm D. 1.8 cm
7. In triangle MNO given below, draw the perpendicular bisector of NO to meet NO at Q. Draw the bisector of angle MNO to meet the perpendicular bisector at P.
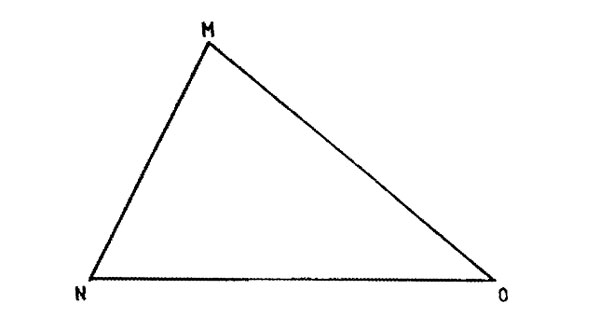
What is the size of the angle MPN?
A. 600 B. 900 C. 300 D. 1500
8. Construct a semi-circle whose diameter AB is given below. Complete triangle ABC in the semi-circle such that angle BAC = 300 and C is on the circumference. Construct a perpendicular CD from C to AB.

What is the length of CD?
A. 6.8 cm B. 5.8 cm C. 4.0 cm D. 3.4 cm
9. In the figure below, construct the bisector of angle PQR. On the same figure, construct the perpendicular bisector of line QR. Let the bisectors meet at S.
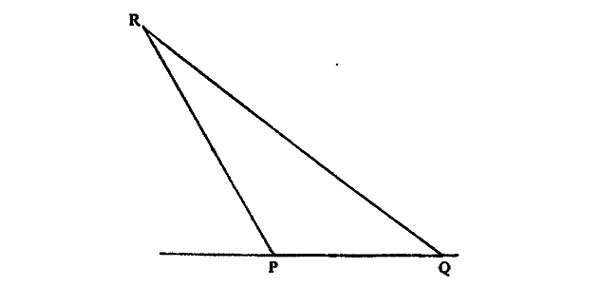
What is the size of the line QS?
A. 5.5 cm B. 5.2 cm C. 4.6 cm D. 1.5 cm
10. On the diagram below, draw the bisector of angle PQR. Draw the perpendicular bisector of line QR to cut the angle bisector at S, line QP at T and line QR at U.
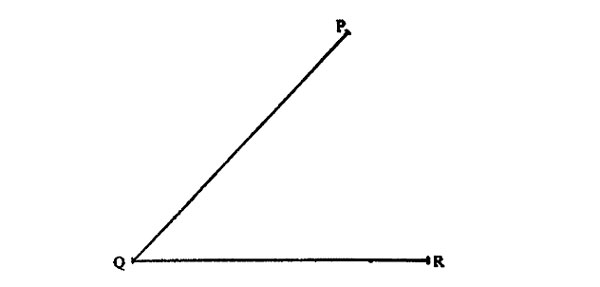
What is the length of ST in centimeters?
A. 5.0 B. 3.6 C. 2.1 D. 1.5
11. In the quadrilateral MNPQ below, draw a perpendicular from M to meet line NP at R. Draw line QR.
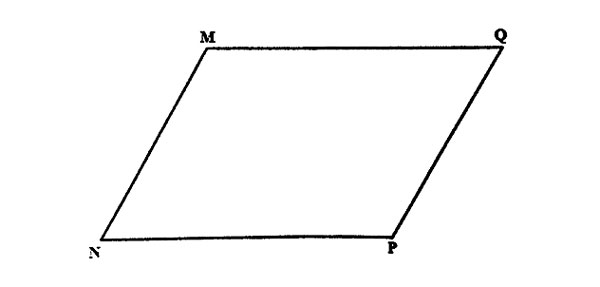
What is the size of the angle MQR?
A. 600 B. 570 C. 330 D. 270